計算整數數組中的山丘和山谷
一、簡介
在解決資料結構和演算法 (DSA) 問題時,計算序列中的不同模式可能會很有趣。在上一篇文章中,我們討論了在整數列表中發現峰值元素的各種方法,這些方法提供了不同的時間複雜度,例如 O(log n) 或 O(n)。
在本文中,我們將解決一個常見問題,涉及識別和計算整數數組中的山丘和山谷。這個問題是磨練我們在 Java 中數組遍歷和條件檢查技能的一個極好的方法。我們將透過解決方案、程式碼範例和解釋來逐步探索該問題。
2. 問題陳述
給定一個整數數組,我們需要識別並計算所有的山丘和山谷。
我們是這樣定義它們的:
- Hill:相鄰元素的序列,其中序列以較低的數字開始,以較高的數字達到峰值,然後以較低的數字結束。
- 谷:相反的模式,序列從高位開始,下降到較低值,然後回升。
簡而言之,數組中的山是一個峰,兩側都有較低的元素,而谷是一個槽,兩側都有較高的元素。
此外,我們應該注意,具有相同值的相鄰索引屬於同一山丘或山谷。
最後,要將索引分類為山丘或山谷的一部分,它的左側和右側必須有不相等的鄰居。這也意味著我們將一次專注於三個指數來製作一座山或一座山谷。
2.1.例子
為了更好地理解山丘和山谷的概念,讓我們來看看下面的例子。
Input array: [4, 5, 6, 5, 4, 5, 4]讓我們逐步瀏覽數組,根據我們的定義來識別山丘和山谷。
角點索引 0 和 6:由於第一個和最後一個索引分別沒有左鄰居和右鄰居,因此它們不能形成任何山或谷。因此,我們將忽略它們。
索引 1 ( 5 ): 5的最近的非相等鄰居是4 (左)和6 (右)。 5不大於兩個鄰居(因此它不是山),也不小於兩個鄰居(因此它不是山谷)。
索引 2 ( 6 ):它的鄰居是5 (左)和5 (右)。 6比6, 5 5 。
索引 3 ( 5 ):鄰居是6 (左)和4 (右)。由於5小於6且大於4 ,因此它既不是山也不是山谷。
對於索引 4 ( 4 ):它的鄰居是5 (左)和5 (右)。由於4小於兩個鄰居,因此它顯然形成了一個山谷 [ 5, 4, 5 ]。
索引 5 ( 5 ):鄰居是4 (左)和4 (右)。 5比兩個鄰居都大,所以這形成了另一座山 [ 4, 5, 4 ]。
因此,數組 [ 4, 5, 6, 5, 4, 5, 4 ] 的輸出應該是 3。
2.2.圖形表示
讓我們在顯示山丘和山谷的圖表上繪製數組numbers [ 4, 5, 6, 5, 4, 5, 4 ],其中 x 軸表示索引,y 軸顯示每個索引處的值。我們將用虛線連接這些點以直觀地表示山丘和山谷:
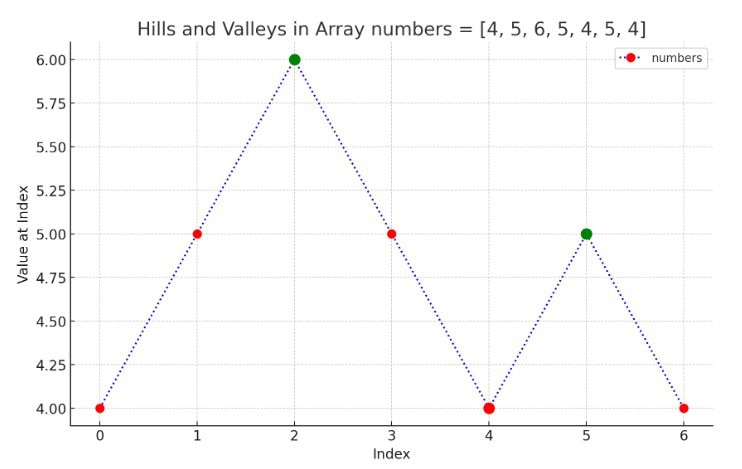
綠色標記表示“山丘”,其中值高於其兩個相鄰點,紅色標記表示“山谷”,其中值低於其兩個相鄰點。
這張圖清楚地顯示我們有兩座山和一處山谷。
3. 演算法
讓我們定義一個演算法來識別和計算給定數組中的所有山丘和山谷來解決這個問題:
1. Accept an array of integers, let's call it numbers.
2. Loop through numbers from the second element to the second-to-last element.
3. For each element at index i:
Let prev be numbers[i-1], current be numbers[i], and next be numbers[i+1].
4. When consecutive equal elements are encountered, skip over them while maintaining the last seen value.
5. Identify Hills:
If current is greater than both prev and next, it's a hill.
Increment hill count.
6. Identify Valleys:
If current is less than both prev and next, it's a valley.
Increment valley count.
7. Repeat Steps 3–6 until the end of the array.
8. Return the sum of hills and valley.因此,我們可以使用該演算法有效地檢測所有的山丘和山谷。請注意,我們只需要一次遍歷數字數組。
4. 實施
現在,讓我們用 Java 實作這個演算法:
int countHillsAndValleys(int[] numbers) {
int hills = 0;
int valleys = 0;
for (int i = 1; i < numbers.length - 1; i++) {
int prev = numbers[i - 1];
int current = numbers[i];
int next = numbers[i + 1];
while (i < numbers.length - 1 && numbers[i] == numbers[i + 1]) {
// skip consecutive duplicate elements
i++;
}
if (i != numbers.length - 1) {
// update the next value to the first distinct neighbor only if it exists
next = numbers[i + 1];
}
if (current > prev && current > next) {
hills++;
} else if (current < prev && current < next) {
valleys++;
}
}
return hills + valleys;
}在這裡,在count HillsAndValleys()方法中,我們有效地識別和計算給定整數數組中的山丘和山谷。首先,我們從第二個元素開始迭代數組索引,到倒數第二個元素結束。這確保了我們檢查的每個元素都有左鄰居和右鄰居。
接下來,對於每個索引,我們跳過連續的重複元素以避免冗餘檢查,並確保邏輯準確地應用於由鄰居包圍的分組元素。
對於每個剩餘的索引,我們將**current元素與其鄰居進行比較 - 如果它大於兩個,我們將其識別為一座山;如果它比兩者都小,我們就將其識別為山谷。**
最後,我們返回山丘和山谷的總數。總的來說,這種方法讓我們可以透過避免額外的列表和記憶體使用來優化效能,從而使我們的解決方案高效且簡單。
5. 測試我們的解決方案
讓我們測試我們的邏輯並透過將不同的陣列傳遞給countHillsAndValleys()來解決各種測試案例:
// Test case 1: Our example array
int[] array1 = { 4, 5, 6, 5, 4, 5, 4};
assertEquals(3, countHillsAndValleys(array1));
// Test case 2: Array with strictly increasing elements
int[] array2 = { 1, 2, 3, 4, 5, 6 };
assertEquals(0, countHillsAndValleys(array2));
// Test case 3: Constant array
int[] array3 = { 5, 5, 5, 5, 5 };
assertEquals(0, countHillsAndValleys(array3));
// Test case 4: Array with no hills or valleys
int[] array4 = { 6, 6, 5, 5, 4, 1 };
assertEquals(0, countHillsAndValleys(array4));
// Test case 5: Array with a flatten valley
int[] array5 = { 6, 5, 4, 4, 4, 5, 6 };
assertEquals(1, countHillsAndValleys(array5));
// Test case 6: Array with a flatten hill
int[] array6 = { 1, 2, 4, 4, 4, 2, 1 };
assertEquals(1, countHillsAndValleys(array6));這裡, array2是一個嚴格遞增的數組,因此它沒有任何山丘或山谷**。同樣, array3是一個具有相同元素的常數數組,因此它沒有山丘或山谷。**
6. 複雜度分析
讓我們分析一下我們的解決方案的時間和空間複雜度:
時間複雜度: O(n) ,其中n是數組的長度。函數countHillsAndValleys()迭代數組一次,僅檢查每個元素一次。
空間複雜度: O(1) ,因為我們只為計數器使用固定數量的空間,且不需要任何額外的資料結構。
七、結論
在本教程中,我們探索了一種使用 Java 計算數組中的山丘和山谷的結構化方法。此外,我們還解決了邊緣情況並透過各種測試案例驗證了解決方案。
與往常一樣,本文的源代碼可以在 GitHub 上取得。