Scipy優化算法

scipy.optimize包提供了幾種常用的優化算法。該模塊包含以下幾個方面 -

使用各種算法(例如BFGS，Nelder-Mead單純形，牛頓共軛梯度，COBYLA或SLSQP)的無約束和約束最小化多元標量函數(minimize())
全局(蠻力)優化程序(例如，anneal()，basinhopping())
最小二乘最小化(leastsq())和曲線擬合(curve_fit())算法
標量單變量函數最小化(minim_scalar())和根查找(newton())
使用多種算法(例如，Powell，Levenberg-Marquardt混合或Newton-Krylov等大規模方法)的多元方程系統求解(root)

多變量標量函數的無約束和約束最小化

minimize()函數爲scipy.optimize中的多變量標量函數提供了無約束和約束最小化算法的通用接口。爲了演示最小化函數，考慮使NN變量的Rosenbrock函數最小化的問題 -
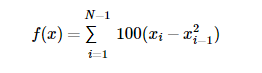
Scipy優化算法

這個函數的最小值是0，當xi = 1時達到。

Nelder–Mead單純形算法

在下面的例子中，minimize()例程與Nelder-Mead單純形算法(method ='Nelder-Mead')一起使用(通過方法參數選擇)。參考下面的例子。

import numpy as np
from scipy.optimize import minimize

def rosen(x):

x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead')

print(res.x)

上述程序將生成以下輸出 -

[7.93700741e+54  -5.41692163e+53  6.28769150e+53  1.38050484e+55  -4.14751333e+54]

簡單算法只需要函數評估，對於簡單的最小化問題是一個不錯的選擇。但是，由於它不使用任何梯度評估，因此可能需要較長時間才能找到最小值。

另一種只需要函數調用來尋找最小值的優化算法就是鮑威爾方法，它可以通過在minimize()函數中設置method ='powell'來實現。

　最小二乘

求解一個帶有變量邊界的非線性最小二乘問題。給定殘差f(x)(n個實變量的m維實函數)和損失函數rho(s)(標量函數)，最小二乘法找到代價函數F(x)的局部最小值。看看下面的例子。

在這個例子中，Rosenbrock函數的最小值不受自變量的限制。

#Rosenbrock Function
def fun_rosenbrock(x):
   return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])

from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)

print (res)

請注意，我們只提供殘差的向量。該算法將成本函數構造爲殘差的平方和，這給出了Rosenbrock()函數。確切的最小值是x = [1.0,1.0]。

上述程序將生成以下輸出 -

active_mask: array([ 0., 0.])
      cost: 9.8669242910846867e-30
      fun: array([ 4.44089210e-15, 1.11022302e-16])
      grad: array([ -8.89288649e-14, 4.44089210e-14])
      jac: array([[-20.00000015,10.],[ -1.,0.]])
   message: '`gtol` termination condition is satisfied.'
      nfev: 3
      njev: 3
   optimality: 8.8928864934219529e-14
      status: 1
      success: True
         x: array([ 1., 1.])

求根

讓我們瞭解求根如何在SciPy中使用。

標量函數

如果有一個單變量方程，則可以嘗試四種不同的尋根算法。這些算法中的每一個都需要預期根的時間間隔的端點(因爲函數會改變符號)。一般來說，brentq是最好的選擇，但其他方法可能在某些情況下或學術目的有用。

定點求解

與找到函數零點密切相關的問題是找到函數的固定點的問題。函數的固定點是函數評估返回點的點:g(x)= x。顯然，gg的不動點是f(x)= g(x)-x的根。等價地，ff的根是g(x)= f(x)+ x的固定點。例程fixed_point提供了一個簡單的迭代方法，使用Aitkens序列加速度來估計gg的固定點，如果給出起點的話。

方程組
使用root()函數可以找到一組非線性方程的根。有幾種方法可供選擇，其中hybr(默認)和lm分別使用Powell的混合方法和MINPACK中的Levenberg-Marquardt方法。

下面的例子考慮了單變量超越方程。
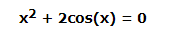
Scipy優化算法

其根可以求解如下 -

import numpy as np
from scipy.optimize import root
def func(x):
   return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)
print (sol)

執行上面示例代碼，得到以下結果 -

fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
   nfev: 10
   qtf: array([ -2.77644574e-12])
      r: array([-3.34722409])
   status: 1
   success: True
      x: array([-0.73908513])

Scipy教程

Nelder–Mead單純形算法

最小二乘

求根

　最小二乘