使用 Choco 進行約束編程

1. 概述

在本教程中，我們將了解Choco-solver ，一個流行的 Java 約束程式設計 (CP) 框架。

總的來說，我們將簡要地了解 CP 的基礎知識，然後查看 Choco-solver 庫的關鍵概念。最後，我們將使用該庫建立一個小程式來解決數獨難題。

2. 約束規劃概念

CP是一種不同於傳統確定性或命令式程式設計的範式，有助於解決組合問題。與約束編程相關的一些用例包括調度、規劃、路由、打包、資源分配和解決數獨難題。

首先，讓我們回顧一下 CP 的主要結構：

• 變數：一組未知數 X 1 , X 2 , X 3 ,…, X n
• 域：未知數的可能值，表示為 D 1 , D 2 , D 3 ,…, D k
• 限制：將域值指派給變數時應滿足的規則或標準，表示為 C 1 , C 2 , C 3 ,…, Cm
• 通常表示為 P = (X, D, C)，其中 P 代表問題

3.前提條件

在開始使用 Choco-solver 之前，讓我們匯入必要的Maven 依賴項：

<dependency>

 <groupId>org.choco-solver</groupId>

 <artifactId>choco-solver</artifactId>

 <version>4.10.14</version>

 </dependency>

4. Choco-solver的關鍵組件

讓我們檢查一下 Choco-solver 框架的關鍵元件。在庫中， Model類別是保存變數和約束的容器或上下文：

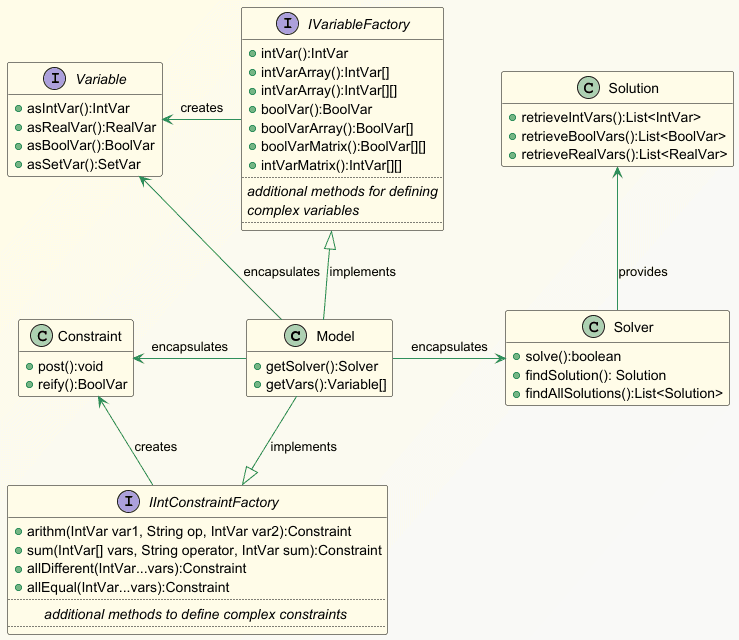
Variable和Constraint類別表示 CP 程式設計範例中的變數和限制。 Model類別實作IVariableFactory接口，包括有效定義變數及其域值的方法。此外，它創建單維和多維域值數組的能力為複雜問題建模提供了出色的靈活性和便利性。

此外， Model類別也實作約束工廠接口，如IIntConstraintFactory 。因此，它的方法（如arithm() 、 sum() 、 allDifferent()等）有助於定義變數之間的算術關係。該庫提供了許多其他方法來設定更複雜的約束。

定義變數和約束後，我們可以呼叫Model#getSolver()方法來取得Solver類別。此外，它的方法如Solver#solve()和Solver#findSolution()有助於獲得解決方案。

此外，本文只是 Choco-solver 函式庫更廣泛功能的預覽。它提供了探索圖書館更複雜功能的動力。

在下一節中，我們將在實現數獨板解決方案時了解更多資訊。

5. 解決空白數獨板

數獨板是一個 9 x 9 矩陣，其中包含九個 3 x 3 矩陣，其唯一值在 1 到 9 之間。

空白的數獨板可以有多種解決方案。我們將每個單元格表示為域值從 1 到 9 的變量，並使用 Choco-solver 庫實現SudokuSolver類別。

5.1.尋找多種解決方案

讓我們來看看SudokuSolver#findSolutions()方法：

List<Integer[][]> findSolutions(final int MAX_SOLUTIONS) {

 IntVar[][] sudokuCells = createModelAndVariables();

 setConstraints(sudokuCells);



 List<Integer[][]> solvedSudokuBoards = getSolutions(MAX_SOLUTIONS);

 return solvedSudokuBoards;

 }

它在 s udokuCells中建立模型及其變數。然後，它對變數設定約束，最終得到解決方案。

5.2.建立模型和變數

createModelAndVariables()方法實例化Model並傳回 9 x 9 矩陣：

IntVar[][] createModelAndVariables() {

 sudokuModel = new Model("Sudoku Solver");

 IntVar[][] sudokuCells = sudokuModel.intVarMatrix("board", 9, 9, 1, 9);

 return sudokuCells;

 }

首先，我們使用標識符Sudoku Solver來建立Model物件。接下來，我們透過在新建立的Model物件上呼叫Model#intVarMatrix()來建立一個二維 9 x 9 矩陣。它包含IntVar變量，其域值範圍為 1 到 9。

5.3.設定變數約束

在下一步中，我們對Model物件的域變數設定約束：

void setConstraints(IntVar[][] sudokuCells) {

 for (int i = 0; i < 9; i++) {

 IntVar[] rowCells = getRowCells(sudokuCells, i);

 sudokuModel.allDifferent(rowCells).post();



 IntVar[] columnCells = getColumnCells(sudokuCells, i);

 sudokuModel.allDifferent(columnCells).post();

 }



 for (int i = 0; i < 9; i += 3) {

 for (int j = 0; j < 9; j += 3) {

 IntVar[] cellsInRange = getCellsInRange(j, j + 2, i, i + 2, sudokuCells);

 sudokuModel.allDifferent(cellsInRange).post();

 }

 }

 }

getRowCells()和getColumnCells()方法分別傳回第i 行和第 i 列中的所有單元格。然後， Model#allDifferent()對數獨板九行九列中檢索到的單元格變數設定約束。它確保域值 1-9 不會在任何行或列中重複。

此外，我們檢索所有 3 x 3 網格的單元格並套用約束以確保其單元格中的值唯一。

5.4.取得解決方案

最後，設定約束後，我們呼叫getSolutions()方法：

List<Integer[][]> getSolutions(int MAX_SOLUTIONS) {

 List<Integer[][]> solvedSudokuBoards = new ArrayList<>();

 int solutionCount = 0;

 while (sudokuModel.getSolver().solve()) {

 if (solutionCount++ > MAX_SOLUTIONS - 1) {

 break;

 }

 IntVar[] solvedSudokuCells = sudokuModel.retrieveIntVars(true);



 solvedSudokuBoards.add(getNineByNineMatrix(solvedSudokuCells));

 sudokuModel.getSolver().reset();

 }

 return solvedSudokuBoards;

 }

此方法傳回多個二維數組，其中包含List中的解決方案。 Model#getSolver()取得Solver對象，在該物件上我們呼叫Solver#solve() to用解填滿Model中的IntVar變數。

稍後，我們透過呼叫Model#retrieveIntVars()來擷取數組中的所有單元格值。在迴圈結束時，我們呼叫Solver#reset()來重置變數值。隨後，該庫在接下來的迭代中將新的解決方案填入變數中。

5.5.結果

現在，讓我們執行SudokuSolver#findSolutions()方法來檢查結果：

void whenSudokuBoardIsEmpty_thenFindTwoSolutions() {

 SudokuSolver sudokuSolver = new SudokuSolver();

 List<Integer[][]> sudokuSolutionMatrices = sudokuSolver.findSolutions(2);

 sudokuSolutionMatrices.forEach(e -> checkValidity(e));

 sudokuSolutionMatrices.forEach(sudokuSolver::printSolution);

 }

該程式有助於為空白數獨板找到兩種可能的解決方案。找到解決方案後，它會呼叫checkValidity()來驗證結果。最後， SudokuSolver#printSolution()方法印出 9 x 9 數獨板：

3 7 2 | 1 5 6 | 4 9 8

 8 4 5 | 2 3 9 | 6 7 1

 1 9 6 | 8 7 4 | 3 2 5

 ---------------------

 5 3 1 | 6 2 7 | 8 4 9

 4 2 9 | 3 8 5 | 7 1 6

 7 6 8 | 4 9 1 | 2 5 3

 ---------------------

 9 1 4 | 7 6 3 | 5 8 2

 6 8 7 | 5 1 2 | 9 3 4

 2 5 3 | 9 4 8 | 1 6 7

同樣，可以檢索並列印多個解決方案。

6. 解決部分解決的數獨板

通常，在數獨謎題中，棋盤是部分填充的。這次我們將以與上一節類似的方式來處理這個問題。但是，將有一個解決方案。

6.1.尋找單一解決方案

對於這樣的場景，我們在SudokuSolver類別中實作findSolution()方法：

Integer[][] findSolution(int[][] preSolvedSudokuMatrix) {

 IntVar[][] sudokuCells = createModelAndVariables();

 setConstraints(sudokuCells, preSolvedSudokuMatrix);



 Solution solution = sudokuModel.getSolver().findSolution();

 IntVar[] solvedSudokuCells = solution.retrieveIntVars(true).toArray(new IntVar[0]);

 return getNineByNineMatrix(solvedSudokuCells);

 }

程式像以前一樣聲明變數並設定約束。但是，與前面的範例不同，它使用附加的二維數組參數來呼叫重載的setConstraints()方法。未解析的單元格在二維preSolvedSudokuMatrix數組中以0值表示。

現在讓我們來看看setConstraints()方法：

void setConstraints(IntVar[][] sudokuCells, int[][] preSolvedSudokuMatrix) {

 setConstraints(sudokuCells);

 for (int i = 0; i < 9; i++) {

 for (int j = 0; j < 9; j++) {

 if (preSolvedSudokuMatrix[i][j] != 0) {

 sudokuCells[i][j].eq(preSolvedSudokuMatrix[i][j])

 .post();

 }

 }

 }

 }

首先，呼叫setConstraints()有助於像以前一樣設定預設約束。然後，從ArExpression介面繼承的eq()方法應用約束來指派preSolvedSudokuMatrix中的預填單元格值。

最後，在SudokuSolver#findSolution()方法中，我們呼叫Solver#findSolution()來取得Solution物件。最終， Solution#retrieveIntVars()幫助檢索填入的儲存格。

6.2.結果

讓我們考慮一個預先填充的數獨板：

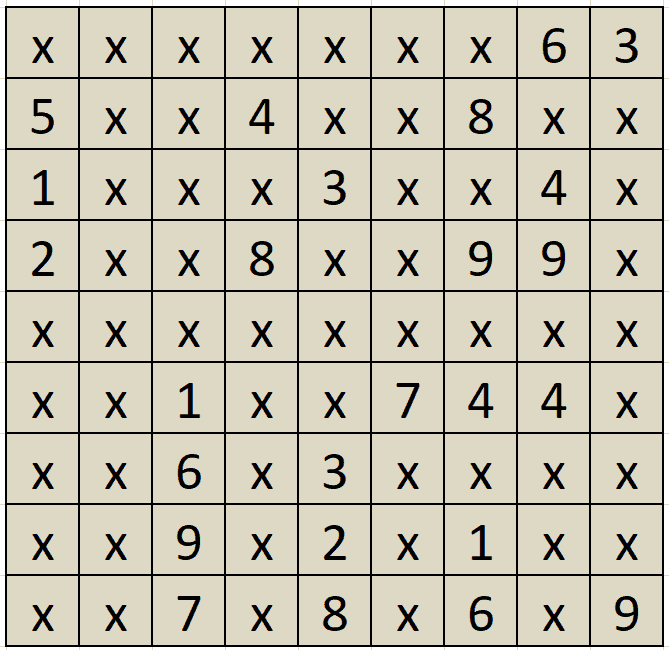
讓我們運行SudokuSolver#findSolution()方法來填入其餘欄位：

void whenSudokuPartiallySolved_thenFindSolution() {

 SudokuSolver sudokuSolver = new SudokuSolver();

 Integer[][] solvedSudokuBoard = sudokuSolver.findSolution(initialValues);



 checkValidity(solvedSudokuBoard);

 sudokuSolver.printSolution(solvedSudokuBoard);

 }

我們使用checkValidity()方法驗證SudokuSolver#findSolution()的結果。此後，我們列印解決方案：

9 8 4 | 7 5 1 | 2 6 3

 5 7 3 | 4 6 2 | 8 9 1

 1 6 2 | 9 3 8 | 5 4 7

 ---------------------

 2 4 5 | 8 1 3 | 9 7 6

 7 9 8 | 6 2 4 | 3 1 5

 6 3 1 | 5 9 7 | 4 2 8

 ---------------------

 8 1 6 | 3 4 9 | 7 5 2

 3 5 9 | 2 7 6 | 1 8 4

 4 2 7 | 1 8 5 | 6 3 9

七、結論

在本文中，我們探索了 Choco-solver，這是一個用於解決組合問題的多功能且富有表現力的開源程式庫。

該庫透過定義變數、它們的域值和約束來幫助幾乎以聲明方式對問題進行建模。因此，它允許我們獲得多種解決方案，而無需編寫任何特定於領域的邏輯。

和往常一樣，本文使用的原始程式碼可以在 GitHub 上參考。