神經網絡

神經網絡是並行計算設備，它們試圖構建大腦的計算機模型。 背後的主要目標是開發一個系統來執行各種計算任務比傳統系統更快。 這些任務包括模式識別和分類，近似，優化和數據聚類。

什麼是人工神經網絡(ANN)

人工神經網絡(ANN)是一個高效的計算系統，其核心主題是借用生物神經網絡的類比。人工神經網絡也被稱爲人工神經系統，並行分佈式處理系統和連接系統。 ANN獲取了大量以某種模式相互連接的單元，以允許它們之間的通信。這些單元也稱爲節點或神經元，是並行操作的簡單處理器。

每個神經元通過連接鏈接與其他神經元連接。每個連接鏈路與具有關於輸入信號的信息的權重相關聯。這是神經元解決特定問題最有用的信息，因爲體重通常會激發或抑制正在傳遞的信號。每個神經元都有其內部狀態，稱爲激活信號。在組合輸入信號和激活規則之後產生的輸出信號可以被髮送到其他單元。

如果想詳細研究神經網絡，那麼可以參考以下示例 - 人工神經網絡。

安裝有用的包

在Python中創建神經網絡，可以使用一個強大的NeuroLab神經網絡包。它是一個基本的神經網絡算法庫，具有靈活的網絡配置和Python學習算法。可以在命令提示符下使用以下命令來安裝此軟件包 -

pip install NeuroLab

如果使用的是Anaconda環境，請使用以下命令安裝NeuroLab -

conda install -c labfabulous neurolab

構建神經網絡

在本節中，讓我們使用NeuroLab軟件包在Python中構建一些神經網絡。

基於感知器的分類器

感知器是ANN的基石。 如果您想了解更多關於Perceptron的信息，可以點擊鏈接 - artificial_neural_network

以下是逐步執行Python代碼，用於構建基於感知器的簡單神經網絡分類器 -

如下所示導入必要的軟件包 -

import matplotlib.pyplot as plt
import neurolab as nl

請注意，這是一個監督學習的例子，因此您也必須提供目標值。

input = [[0, 0], [0, 1], [1, 0], [1, 1]]
target = [[0], [0], [0], [1]]

用2個輸入和1個神經元創建網絡 -

net = nl.net.newp([[0, 1],[0, 1]], 1)

現在，訓練網絡。 在這裏使用Delta規則進行訓練。

error_progress = net.train(input, target, epochs=100, show=10, lr=0.1)

接下來，可視化輸出並繪製圖表 -

plt.figure()
plt.plot(error_progress)
plt.xlabel('Number of epochs')
plt.ylabel('Training error')
plt.grid()
plt.show()

可以看到下圖顯示了使用錯誤度量標準的訓練進度 -

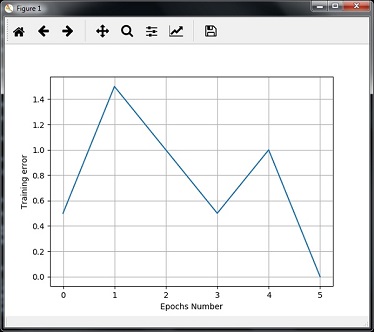
單層神經網絡

在這個例子中，我們來創建一個單層神經網絡，它由獨立的神經元組成，這些神經元在輸入數據上起作用以產生輸出。 請注意，這裏使用neural_simple.txt文件作爲輸入。

如下所示導入所需的軟件包 -

import numpy as np
import matplotlib.pyplot as plt
import neurolab as nl

加載數據集如下代碼 -

input_data = np.loadtxt(「/Users/admin/neural_simple.txt')

以下是我們要使用的數據。 請注意，在此數據中，前兩列是特徵，最後兩列是標籤。

array([[2. , 4. , 0. , 0. ],
      [1.5, 3.9, 0. , 0. ],
      [2.2, 4.1, 0. , 0. ],
      [1.9, 4.7, 0. , 0. ],
      [5.4, 2.2, 0. , 1. ],
      [4.3, 7.1, 0. , 1. ],
      [5.8, 4.9, 0. , 1. ],
      [6.5, 3.2, 0. , 1. ],
      [3. , 2. , 1. , 0. ],
      [2.5, 0.5, 1. , 0. ],
      [3.5, 2.1, 1. , 0. ],
      [2.9, 0.3, 1. , 0. ],
      [6.5, 8.3, 1. , 1. ],
      [3.2, 6.2, 1. , 1. ],
      [4.9, 7.8, 1. , 1. ],
      [2.1, 4.8, 1. , 1. ]])

現在，將這四列分成2個數據列和2個標籤 -

data = input_data[:, 0:2]
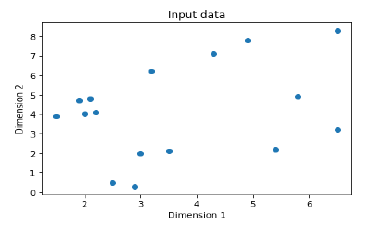
labels = input_data[:, 2:]

使用以下命令繪製輸入數據 -

plt.figure()
plt.scatter(data[:,0], data[:,1])
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Input data')

現在，爲每個維度定義最小值和最大值，如下所示 -

dim1_min, dim1_max = data[:,0].min(), data[:,0].max()
dim2_min, dim2_max = data[:,1].min(), data[:,1].max()

接下來，如下定義輸出層中神經元的數量 -

nn_output_layer = labels.shape[1]

現在，定義一個單層神經網絡 -

dim1 = [dim1_min, dim1_max]
dim2 = [dim2_min, dim2_max]
neural_net = nl.net.newp([dim1, dim2], nn_output_layer)

訓練神經網絡的時代數和學習率如下所示 -

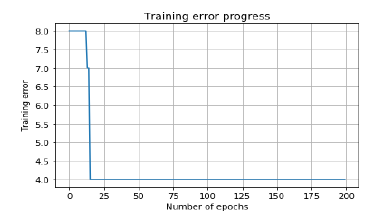
error = neural_net.train(data, labels, epochs = 200, show = 20, lr = 0.01)

現在，使用以下命令可視化並繪製訓練進度 -

plt.figure()
plt.plot(error)
plt.xlabel('Number of epochs')
plt.ylabel('Training error')
plt.title('Training error progress')
plt.grid()
plt.show()

現在，使用上述分類器中的測試數據點 -

print('\nTest Results:')
data_test = [[1.5, 3.2], [3.6, 1.7], [3.6, 5.7],[1.6, 3.9]] for item in data_test:
   print(item, '-->', neural_net.sim([item])[0])

下面是測試結果 -

[1.5, 3.2] --> [1. 0.]
[3.6, 1.7] --> [1. 0.]
[3.6, 5.7] --> [1. 1.]
[1.6, 3.9] --> [1. 0.]

您可以看到迄今爲止討論的代碼的輸出圖表 -

多層神經網絡

在這個例子中，我們創建了一個由多個層組成的多層神經網絡，以提取訓練數據中的基礎模式。 這個多層神經網絡將像一個迴歸器一樣工作。 我們將根據下面等式生成一些數據點:y = 2x2 + 8。

如下所示導入必要的軟件包 -

import numpy as np
import matplotlib.pyplot as plt
import neurolab as nl

根據上述公式生成一些數據點 -

min_val = -30
max_val = 30
num_points = 160
x = np.linspace(min_val, max_val, num_points)
y = 2 * np.square(x) + 8
y /= np.linalg.norm(y)

現在，重塑這個數據集如下 -

data = x.reshape(num_points, 1)
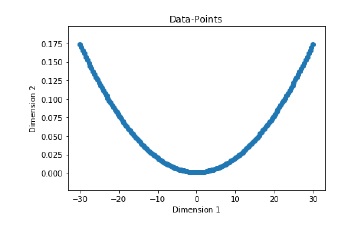
labels = y.reshape(num_points, 1)

使用以下命令可視化並繪製輸入數據集 -

plt.figure()
plt.scatter(data, labels)
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Data-points')

現在，構建神經網絡，其具有兩個隱藏層，第一隱藏層中具有十個神經元的神經元，第二隱藏層中六個，輸出層中一個神經元。

neural_net = nl.net.newff([[min_val, max_val]], [10, 6, 1])

現在使用梯度訓練算法 -

neural_net.trainf = nl.train.train_gd

現在訓練網絡的目標是學習上面生成的數據 -

error = neural_net.train(data, labels, epochs = 1000, show = 100, goal = 0.01)

訓練數據點上運行神經網絡 -

output = neural_net.sim(data)
y_pred = output.reshape(num_points)

現在繪圖並可視化任務 -

plt.figure()
plt.plot(error)
plt.xlabel('Number of epochs')
plt.ylabel('Error')
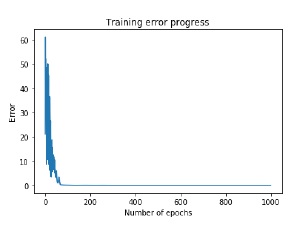
plt.title('Training error progress')

現在將繪製實際與預測輸出關係圖 -

x_dense = np.linspace(min_val, max_val, num_points * 2)
y_dense_pred = neural_net.sim(x_dense.reshape(x_dense.size,1)).reshape(x_dense.size)
plt.figure()
plt.plot(x_dense, y_dense_pred, '-', x, y, '.', x, y_pred, 'p')
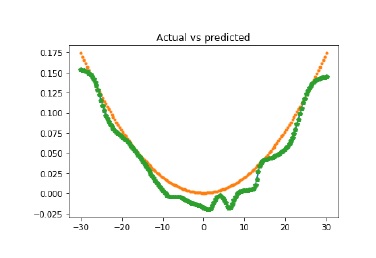
plt.title('Actual vs predicted')
plt.show()

執行上述代碼，您可以觀察如下所示的圖形 -