二叉搜索樹

二叉搜索樹表現出特殊的行爲。一個節點的左子必須具備值小於它的父代值，並且節點的右子節點的值必須大於它的父值。

二叉搜索樹表示

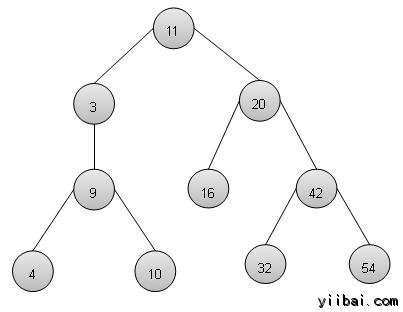
Binary

我們將使用節點對象來實現樹，並通過引用連接它們。

基本操作

以下是遵循樹的基本操作。

搜索 − 搜索一棵樹中的元素。
插入 − 插入元素到一棵樹中。
前序遍歷 − 遍歷一棵樹方法。
後序遍歷 − 遍歷樹在序方法。
後序遍歷 − 遍歷樹的後序方法。

節點

限定了具有一些數據，引用其左，右子節點的節點。

struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};

搜索操作

每當一個元素是被搜索。開始從根節點搜索，如果數據小於鍵值，在左子樹中搜索元素，否則搜索元素在右子樹。每一個節點按照同樣的算法。

struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");

while(current->data != data){
if(current != NULL) {
printf("%d ",current->data);

     //go to left tree
     if(current->data > data){
        current = current->leftChild;
     }//else go to right tree
     else{                
        current = current->rightChild;
     }

     //not found
     if(current == NULL){
        return NULL;
     }
  }

}
return current;
}

插入操作

每當一個元素將被插入。首先找到它應有的位置。開始從根節點搜索，如果數據小於鍵值，搜索空位置在左子樹那麼插入數據。否則，搜索空位置在右子樹並插入數據。

void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;

tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;

//if tree is empty
if(root == NULL){
root = tempNode;
}else{
current = root;
parent = NULL;

  while(1){                
     parent = current;

     //go to left of the tree
     if(data < parent->data){
        current = current->leftChild;                
        //insert to the left
        if(current == NULL){
           parent->leftChild = tempNode;
           return;
        }
     }//go to right of the tree
     else{
        current = current->rightChild;
        //insert to the right
        if(current == NULL){
           parent->rightChild = tempNode;
           return;
        }
     }
  }

}
}

數據結構和算法教程

二叉搜索樹表示

基本操作

節點

搜索操作

插入操作