Java技術Web開發高級語言其他技術腳本語言數據庫大數據教程XML技術專業教育框架軟件工具教程通信技術微軟技術軟件測試手機開發前端技術人工智能實例代碼

數據結構和算法教學
環境設置
數據結構算法基礎
數據結構漸近分析
數據結構基本概念
數組
哈希表
哈希表實例程序（C語言）
鏈表
鏈表實例程序（C語言）
雙向鏈表
循環鏈表
循環鏈表實例程序（C語言）
堆棧
堆棧實例代碼（C語言）
表達式分析
隊列
隊列實例代碼（C語言）
隊列優先級
線性搜索(查找)
線性搜索實例程序（C語言）
二進制搜索(查找)
二進制搜索/查找程序（C語言）
冒泡排序算法
冒泡排序算法實例程序（C語言）
插入排序
選擇排序
選擇排序實例程序（C語言）
合併排序算法
合併排序算法實例程序（C語言）
希爾排序
希爾排序實例程序（C程序）
快速排序
快速排序實例程序（C語言）
圖數據結構
深度優先遍歷
廣度優先遍歷
樹（二叉樹）
樹遍歷
二叉搜索樹
堆
遞歸基礎知識
廣度優先遍歷
樹遍歷

樹（二叉樹）

瀏覽人數：576最近更新：

樹表示由邊緣連接的節點。我們將要具體地討論二叉樹或二叉搜索樹。

二叉樹是用於數據存儲目的的特殊的數據結構。二叉樹有一個特殊的情況，每個節點可以有兩個子節點。二叉樹有序數組和鏈表的兩個好處，搜索排序在數組插入或刪除操作一樣快的，在鏈表也是儘可能快。

樹（二叉樹）

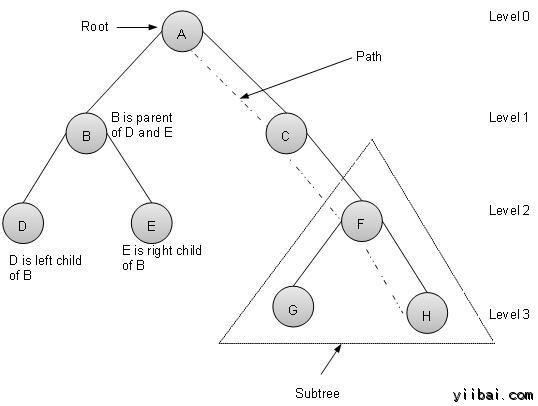
術語

以下是關於樹的重要方面。

  • 路徑 − 路徑是指沿一棵樹的邊緣節點的序列。

  • 根 − 節點在樹的頂部被稱爲根。有每棵樹只有一個根和一個路徑從根節點到任何節點。

  • 父子點 − 除根節點的任何一個節點都有一個邊緣向上的節點稱爲父節點。

  • 子節點 − 給定節點的邊緣部分連接向下以下節點被稱爲它的子節點。

  • 葉子點 − 節點不具有任何子節點被稱爲葉節點。

  • 子樹 − 子樹代表一個節點的後代。

  • 訪問 − 訪問是指檢查某個節點的值在控制的節點上時。

  • 遍歷 − 遍歷意味着通過節點傳遞一個特定的順序。

  • 層次 − 一個節點的層次表示的節點的產生。如果根節點的級別是0，那麼它的下一子結點爲1級，其孫子是2級等。

  • 鍵 − 鍵表示基於一個節點在其上的搜索操作將被進行了一個節點的值。

二叉搜索樹表現出特殊的行爲。一個節點的左子的值必須低於其父的值，節點的右子節點的值必須大於它的父節點的值。

二叉搜索樹表示

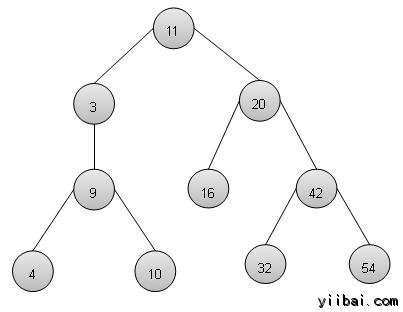
Binary

我們將使用節點對象來實現樹，並通過引用連接它們。

基本操作

以下是遵循樹的基本操作。

  • 搜索 − 搜索一棵樹中的元素

  • 插入 − 插入元素到一棵樹中

  • 前序遍歷 − 遍歷樹前序方法

  • 中序遍歷 − 遍歷樹在序方法

  • 後序遍歷− 遍歷樹的後序方法

節點

限定了具有一些數據，引用其左，右子節點的節點。

struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};

搜索操作

每當一個元素被搜索。開始從根節點搜索後，如果數據小於鍵值，在左子樹中搜索元素，否則在右子樹搜索元素。每一個節點按照同樣的算法。

struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");

while(current->data != data){
if(current != NULL)
printf("%d ",current->data);
//go to left tree

     if(current->data > data){
        current = current->leftChild;
     }//else go to right tree
     else{                
        current = current->rightChild;
     }

     //not found
     if(current == NULL){
        return NULL;
     }

  return current;

}
}

插入操作

每當一個元素被插入。首先找到它應有的位置。從根節點開始搜索，那麼如果數據小於鍵值，在搜索左子樹空位置並插入數據。否則，在右子樹搜索空位置並插入數據。

void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;

tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;

//if tree is empty
if(root == NULL){
root = tempNode;
}else{
current = root;
parent = NULL;

  while(1){                
     parent = current;

     //go to left of the tree
     if(data < parent->data){
        current = current->leftChild;                
        //insert to the left
        if(current == NULL){
           parent->leftChild = tempNode;
           return;
        }
     }//go to right of the tree
     else{
        current = current->rightChild;
        //insert to the right
        if(current == NULL){
           parent->rightChild = tempNode;
           return;
        }
     }
  }

}
}

前序遍歷

這是一個簡單的三個步驟。

  • 訪問根結點
  • 遍歷左子樹
  • 遍歷右子樹

void preOrder(struct node* root){
if(root != NULL){
printf("%d ",root->data);
preOrder(root->leftChild);
preOrder(root->rightChild);
}
}

中序遍歷

這是一個簡單的三個步驟。

  • 遍歷左子樹
  • 訪問根結點
  • 遍歷右子樹

void inOrder(struct node* root){
if(root != NULL){
inOrder(root->leftChild);
printf("%d ",root->data);
inOrder(root->rightChild);
}
}

後序遍歷

這是一個簡單的三個步驟。

  • 遍歷左子樹
  • 遍歷右子樹
  • 訪問根結點

void postOrder(struct node* root){
if(root != NULL){
postOrder(root->leftChild);
postOrder(root->rightChild);
printf("%d ",root->data);
}
}

演示程序

TreeDemo.c

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};

struct node *root = NULL;

void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;

tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;

//if tree is empty
if(root == NULL){
root = tempNode;
}else{
current = root;
parent = NULL;

  while(1){                
     parent = current;

     //go to left of the tree
     if(data < parent->data){
        current = current->leftChild;                
        //insert to the left
        if(current == NULL){
           parent->leftChild = tempNode;
           return;
        }
     }//go to right of the tree
     else{
        current = current->rightChild;
        //insert to the right
        if(current == NULL){
           parent->rightChild = tempNode;
           return;
        }
     }
  }

}
}

struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");

while(current->data != data){
if(current != NULL)
printf("%d ",current->data); 

     //go to left tree
     if(current->data > data){
        current = current->leftChild;
     }//else go to right tree
     else{                
        current = current->rightChild;
     }

     //not found
     if(current == NULL){
        return NULL;
     }
  }

return current;
}

void preOrder(struct node* root){
if(root != NULL){
printf("%d ",root->data);
preOrder(root->leftChild);
preOrder(root->rightChild);
}
}

void inOrder(struct node* root){
if(root != NULL){
inOrder(root->leftChild);
printf("%d ",root->data);
inOrder(root->rightChild);
}
}

void postOrder(struct node* root){
if(root != NULL){
postOrder(root->leftChild);
postOrder(root->rightChild);
printf("%d ",root->data);
}
}

void traverse(int traversalType){
switch(traversalType){
case 1:
printf("\nPreorder traversal: ");
preOrder(root);
break;
case 2:
printf("\nInorder traversal: ");
inOrder(root);
break;
case 3:
printf("\nPostorder traversal: ");
postOrder(root);
break;
}
}

int main() {
/* 11 //Level 0
*/
insert(11);

/* 11 //Level 0
* |
* |---20 //Level 1
*/
insert(20);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
*/
insert(3);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
*/
insert(42);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
* |
* |--54 //Level 3
*/
insert(54);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* |--54 //Level 3
*/
insert(16);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
insert(32);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
insert(9);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--| 32--|--54 //Level 3
*/
insert(4);

/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--|--10 32--|--54 //Level 3
*/
insert(10);

struct node * temp = search(32);
if(temp != NULL){
printf("Element found.\n");
printf("( %d )",temp->data);
printf("\n");
}else{
printf("Element not found.\n");
}

struct node *node1 = search(2);
if(node1 != NULL){
printf("Element found.\n");
printf("( %d )",node1->data);
printf("\n");
}else{
printf("Element not found.\n");
}

//pre-order traversal
//root, left ,right
traverse(1);

//in-order traversal
//left, root ,right
traverse(2);

//post order traversal
//left, right, root
traverse(3);
}

如果我們編譯並運行上述程序，那麼這將產生以下結果 -

Visiting elements: 11 20 42 Element found.(32)
Visiting elements: 11 3 Element not found.

Preorder traversal: 11 3 9 4 10 20 16 42 32 54
Inorder traversal: 3 4 9 10 11 16 20 32 42 54
Postorder traversal: 4 10 9 3 16 32 54 42 20 11

廣度優先遍歷
樹遍歷