NumPy - 線性代數

NumPy 包包含numpy.linalg模塊，提供線性代數所需的所有功能。 此模塊中的一些重要功能如下表所述。

序號

函數及描述

1.

dot 兩個數組的點積

2.

vdot 兩個向量的點積

3.

inner 兩個數組的內積

4.

matmul 兩個數組的矩陣積

5.

determinant 數組的行列式

6.

solve 求解線性矩陣方程

7.

inv 尋找矩陣的乘法逆矩陣

numpy.dot()

此函數返回兩個數組的點積。 對於二維向量，其等效於矩陣乘法。 對於一維數組，它是向量的內積。 對於 N 維數組，它是a的最後一個軸上的和與b的倒數第二個軸的乘積。

import numpy.matlib 
import numpy as np 

a = np.array([[1,2],[3,4]]) 
b = np.array([[11,12],[13,14]]) 
np.dot(a,b)

輸出如下：

[[37  40] 
 [85  92]]

要注意點積計算爲：

[[1*11+2*13, 1*12+2*14],[3*11+4*13, 3*12+4*14]]

numpy.vdot()

此函數返回兩個向量的點積。 如果第一個參數是複數，那麼它的共軛複數會用於計算。 如果參數id是多維數組，它會被展開。

例子

import numpy as np 
a = np.array([[1,2],[3,4]]) 
b = np.array([[11,12],[13,14]]) 
print np.vdot(a,b)

輸出如下：

130

注意：1*11 + 2*12 + 3*13 + 4*14 = 130。

numpy.inner()

此函數返回一維數組的向量內積。 對於更高的維度，它返回最後一個軸上的和的乘積。

例子

import numpy as np 
print np.inner(np.array([1,2,3]),np.array([0,1,0])) 
# 等價於 1*0+2*1+3*0

輸出如下：

2

例子

# 多維數組示例 
import numpy as np 
a = np.array([[1,2], [3,4]]) 

print '數組 a：' 
print a 
b = np.array([[11, 12], [13, 14]]) 

print '數組 b：' 
print b 

print '內積：' 
print np.inner(a,b)

輸出如下：

數組 a：
[[1 2]
[3 4]]

數組 b：
[[11 12]
[13 14]]

內積：
[[35 41]
[81 95]]

上面的例子中，內積計算如下：

1*11+2*12, 1*13+2*14 
3*11+4*12, 3*13+4*14

numpy.matmul

numpy.matmul()函數返回兩個數組的矩陣乘積。 雖然它返回二維數組的正常乘積，但如果任一參數的維數大於2，則將其視爲存在於最後兩個索引的矩陣的棧，並進行相應廣播。

另一方面，如果任一參數是一維數組，則通過在其維度上附加 1 來將其提升爲矩陣，並在乘法之後被去除。

例子

# 對於二維數組，它就是矩陣乘法
import numpy.matlib 
import numpy as np 

a = [[1,0],[0,1]] 
b = [[4,1],[2,2]] 
print np.matmul(a,b)

輸出如下：

[[4  1] 
 [2  2]]

例子

# 二維和一維運算
import numpy.matlib 
import numpy as np 

a = [[1,0],[0,1]] 
b = [1,2] 
print np.matmul(a,b) 
print np.matmul(b,a)

輸出如下：

[1  2] 
[1  2]

例子

# 維度大於二的數組 
import numpy.matlib 
import numpy as np 

a = np.arange(8).reshape(2,2,2) 
b = np.arange(4).reshape(2,2) 
print np.matmul(a,b)

輸出如下：

[[[2   3] 
   [6   11]] 
  [[10  19] 
   [14  27]]]

numpy.linalg.det()

行列式在線性代數中是非常有用的值。 它從方陣的對角元素計算。 對於 2×2 矩陣，它是左上和右下元素的乘積與其他兩個的乘積的差。

換句話說，對於矩陣[[a，b]，[c，d]]，行列式計算爲ad-bc。 較大的方陣被認爲是 2×2 矩陣的組合。

numpy.linalg.det()函數計算輸入矩陣的行列式。

例子

import numpy as np
a = np.array([[1,2], [3,4]]) 
print np.linalg.det(a)

輸出如下：

-2.0

例子

b = np.array([[6,1,1], [4, -2, 5], [2,8,7]]) 
print b 
print np.linalg.det(b) 
print 6*(-2*7 - 5*8) - 1*(4*7 - 5*2) + 1*(4*8 - -2*2)

輸出如下：

[[ 6 1 1]
 [ 4 -2 5]
 [ 2 8 7]]

-306.0

-306

numpy.linalg.solve()

numpy.linalg.solve()函數給出了矩陣形式的線性方程的解。

考慮以下線性方程：

x + y + z = 6

2y + 5z = -4

2x + 5y - z = 27

可以使用矩陣表示爲：

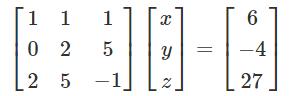
如果矩陣成爲A、X和B，方程變爲：

AX = B

或

X = A^(-1)B

numpy.linalg.inv()

我們使用numpy.linalg.inv()函數來計算矩陣的逆。 矩陣的逆是這樣的，如果它乘以原始矩陣，則得到單位矩陣。

例子

import numpy as np 

x = np.array([[1,2],[3,4]]) 
y = np.linalg.inv(x) 
print x 
print y 
print np.dot(x,y)

輸出如下：

[[1 2]                                                                        
 [3 4]]                                                                       
[[-2.   1. ]                                                                  
 [ 1.5 -0.5]]                                                                 
[[  1.00000000e+00   1.11022302e-16]                                          
 [  0.00000000e+00   1.00000000e+00]]

例子

現在讓我們在示例中創建一個矩陣A的逆。

import numpy as np 
a = np.array([[1,1,1],[0,2,5],[2,5,-1]]) 

print '數組 a：'
print a 
ainv = np.linalg.inv(a) 

print 'a 的逆：' 
print ainv  

print '矩陣 b：' 
b = np.array([[6],[-4],[27]]) 
print b 

print '計算：A^(-1)B：' 
x = np.linalg.solve(a,b) 
print x  
# 這就是線性方向 x = 5, y = 3, z = -2 的解

輸出如下：

數組 a：
[[ 1 1 1]
 [ 0 2 5]
 [ 2 5 -1]]

a 的逆：
[[ 1.28571429 -0.28571429 -0.14285714]
 [-0.47619048 0.14285714 0.23809524]
 [ 0.19047619 0.14285714 -0.0952381 ]]

矩陣 b：
[[ 6]
 [-4]
 [27]]

計算：A^(-1)B：
[[ 5.]
 [ 3.]
 [-2.]]

結果也可以使用下列函數獲取

x = np.dot(ainv,b)